Scottの定理・可測基数とL
集合論雑記目次
今日は Scott(1961) による
「可測基数が存在すれば
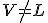 である」ことの証明です。
である」ことの証明です。
この定理は可測基数の重要性とおそらく整合性に関する直感に対し決定的な影
響を与えたと思われるのですが、超巾とその推移的崩壊のテクニックを応用す
ることに気がついた段階で、証明自体は比較的簡単だったのではと推測される
のです。個人的な見解ですが一種の「引き出し論法」です(*1)。
まず
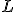 に関する前提条件ですが、今回使用するのは次の事実のみです。
に関する前提条件ですが、今回使用するのは次の事実のみです。
(1)
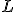 は
最小の内部モデルである。すなわち
は
最小の内部モデルである。すなわち
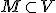 が推移的で、すべての順序数が
が推移的で、すべての順序数が
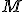 の要素である集合論の
の要素である集合論の
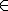 モデルのとき
モデルのとき
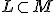
超べきの定義、可測基数の定義、到達不可能であること、可算完備との関連については
測度と可測基数
最小の可測基数
可測基数が到達不可能であること
超積、超べきとLośの定理
を参照して下さい。
一般にクラス(と構造)
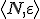 に対し、一対一関数
に対し、一対一関数
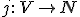 が初等的埋め込み(elementary embedding)であるとは、次の事実が成立すること
でした。
が初等的埋め込み(elementary embedding)であるとは、次の事実が成立すること
でした。
任意の論理式
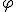 と
と
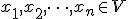 に対し
に対し
~\leftrightarrow~\langle~N,\varepsilon~\rangle~|=~\varphi(j(x_1),j(x_2),\cdots,j(x_n)).)
特に
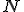 が
推移的崩壊の条件
を満たしている場合、推移的なクラス
が
推移的崩壊の条件
を満たしている場合、推移的なクラス
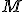 と同型
と同型
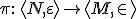 が存在します。
この場合
が存在します。
この場合
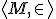 は内部モデルとなり
は内部モデルとなり
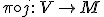 が初等的埋め込み(elementary embedding)となります。一般に推移的な
が初等的埋め込み(elementary embedding)となります。一般に推移的な
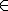 モデルに関する初等的埋め込み(この様に書いた場合恒等関数でなないものとする)
モデルに関する初等的埋め込み(この様に書いた場合恒等関数でなないものとする)
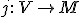 に対し次の事実が成立します。
に対し次の事実が成立します。
(2)
)
(3)
) を満たす
を満たす
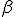 が存在する。このような
が存在する。このような
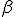 で最小のものを
で最小のものを
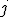 の critical point と言い
の critical point と言い
) と表す。
と表す。
(2)は整列順序集合間の増加関数の性質から導かれます。(3)の証明は省略しま
す(*2)。ただしこれから展開する具体例では確かに可測基数が critical
point となります。
Scott の定理の証明ですが、
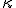 を最小の可測基数とし、
を最小の可測基数とし、
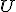 を
を
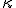 上の nonprincipal
上の nonprincipal
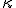 -complete ultrafilter とします。超巾
-complete ultrafilter とします。超巾
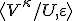 を考えると
を考えると
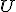 が可算完備であることにより推移的崩壊
が可算完備であることにより推移的崩壊
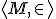 を考えることが可能で、初等的埋め込み
を考えることが可能で、初等的埋め込み
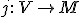 を構成することができ、さらに
を構成することができ、さらに
=\kappa) が成立します。
が成立します。
この事実を仮定すると(後で証明)
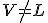 の証明は簡単です。もし
の証明は簡単です。もし
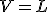 を仮定すると、(1)により
を仮定すると、(1)により
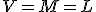 が成立し、
が成立し、
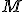 が内部モデルで
が内部モデルで
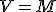 であることにより
であることにより
) ,
,
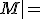 「
「
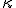 は最小の可測基数」
が成立します。ところが elementary embedding の観点から
は最小の可測基数」
が成立します。ところが elementary embedding の観点から
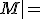 「
「
) は最小の可測基数」が成立するので矛盾です(*3)。
は最小の可測基数」が成立するので矛盾です(*3)。
最後に
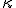 が critical point になることの証明です。
まず
が critical point になることの証明です。
まず
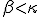 に対し
に対し
) であることですが、
であることですが、
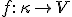 とし、超巾での解釈で
とし、超巾での解釈で
) を仮定します。このとき定義により
を仮定します。このとき定義により
~\in~\beta~\}~\in~U) が成立します。今
が成立します。今
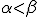 に対し
に対し
~=~\alpha~\}) とし、任意の
とし、任意の
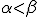 に対し
に対し
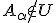 を仮定すると、
を仮定すると、
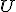 が
が
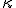 -complete であることにより
-complete であることにより
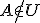 となり矛盾です。従って
となり矛盾です。従って
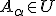 を満たす
を満たす
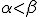 が存在しますが、これは超巾(経由)での解釈で
が存在しますが、これは超巾(経由)での解釈で
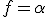 を意味し、従って
を意味し、従って
.)
次に恒等写像
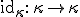 (うるさく言えば
(うるさく言えば
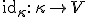 )
の超巾での解釈を考察します。まず超巾での解釈で
)
の超巾での解釈を考察します。まず超巾での解釈で
) は明らかです(恒等写像の各値が
は明らかです(恒等写像の各値が
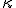 の要素なので)。一方
の要素なので)。一方
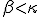 とすると、
とすると、
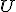 が nonprincipal
が nonprincipal
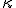 -complete ultrafilter であることにより
-complete ultrafilter であることにより
\}~\in~U) が成立し、
が成立し、
<\mathrm{id}_\kappa.) 従って
従って
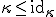 が成立し
が成立し
.)
この定理の証明は(分かってしまえば)簡単ですが、内部モデルの考え、超巾と
その推移的崩壊のご利益を使いきっている感じがします。また超自然数の場合
と同様に恒等写像が
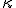 の住人からは「非常に大きく」見える点もなかなか興味深いのです。
の住人からは「非常に大きく」見える点もなかなか興味深いのです。
正則の公理や AFA の話題
から、
超巾や推移的崩壊とそれらの関連性を教えて頂き
、始めて巨大基数の有用性を実感できる定理を理解出来たつもりになっていま
す。数学って楽しいです。
(付記) えーっと Category の方は全然進んでいません。もう少々時間を。
(*1) 証明の一部分は、先週の超
巾と正則性 の
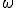 を可測基数
を可測基数
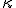 に変えただけであり、論法は非常に良く似ているのに驚きます。もちろん
に変えただけであり、論法は非常に良く似ているのに驚きます。もちろん
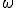 上に
上に
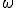 -complete ultrafilter(普通の超フィルター) が存在するという類推が成立
しているから。
-complete ultrafilter(普通の超フィルター) が存在するという類推が成立
しているから。
(*2) 例えば「巨大基数の集合論」を参照して下さい。さらにこの条件が成立
してる場合、critical point は可測基数になることも分かります。
(*3) 初等的埋め込み
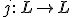 が存在すれば
が存在すれば
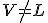 です。
さらに初等的埋め込み
です。
さらに初等的埋め込み
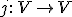 は存在しないことが知られています(Kunen 1971)。
は存在しないことが知られています(Kunen 1971)。
(2006年7月24日追記) 上の「初等的埋め込み」は「定義可能な初等的埋め込み」
とする必要があります。
くるるさんに教えて
頂きました。どうもありがとうございます。
 先日中国のお土産にいもむしを買ってきて下さった H さん
ですが、まだまだおみやげの在庫があったらしく、昨日もらったのが写真のお
菓子。
先日中国のお土産にいもむしを買ってきて下さった H さん
ですが、まだまだおみやげの在庫があったらしく、昨日もらったのが写真のお
菓子。






