Martin の公理の帰結(その２)
[集合論雑記目次]
今日は前回述べたの定理(下に再掲) (c)(d)(e) について証明の概略を記述します。
[定理]
(c)
}\rightarrow)
[
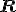の Lebesgue 零集合の
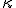個の和は Lebesgue 零集合]
(d)
}\rightarrow[)
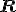の first category sets の
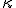個の和は first category]
(e)
~\rightarrow[)
Suslin の仮説が成立する]
[(c) の証明]
まずは (c) の証明の概略ですが、まず Lebesgue 零集合の特徴付けを思い出
します(もう 25年以上やってないから完全に忘れてますな)。
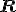の部分集合
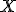が Lebesuge 零集合となる条件は
任意の
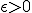に対し
\le\epsilon)
なる開集合
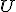が存在すること。ただし
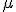は実数直線上の通常の Lebesgue 測度とします。
さて上の
を固定します。
さらに
)
が成立すると仮定して
_{\alpha<\kappa})
を零集合の
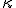列とします。
例のごとく Martin の公理を適用するには、適切な半順序を定義するのが重要
なのですが、この定理の証明には固定された
に対し次の半順序集合を使用します。
\wedge(\mu(p)<\epsilon)\})
半順序は例のごとく
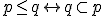にて定義します。容易に分るように
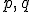が compatible となる条件は
<\epsilon)
となることで、その場合
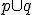が共通の拡張となります。さて
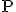が c.c.c を満たすことの証明は後回しにして、次の稠密な集合族を定義しま
す(稠密となることはほとんど明らか)。
)
が成立しているのでフィルター
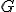が存在し
)
が成立します。このとき
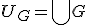を考えると
)
が成立し、したがって
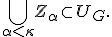さらに実数直線が開集合の可算基底をもつことと
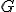がフィルターであることを考慮すると
\le{\epsilon})
が成立することは容易に分ります(
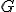の可算個の元で
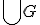を構成できるから)。
最後に残ったのは
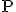が c.c.c を満たすことの証明ですが
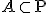を antichain からなる非可算な部分集合として矛盾を導きます。
ところが
<\epsilon-1/n\}\quad~(n~\in~\omega))
を考えると少なくとも一つの
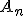は非可算なので、
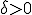を固定して、もともとの
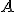が非可算で
<\epsilon-2\delta))
であると仮定しても問題ありません。さて有理数を両端とする有界開
区間の有限個の和集合からなる可算集合を
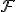とします。このとき次の事実が成立することは、可測集合が
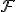の要素で(内側から)いくらでも近似可能であることからほとんど明らかです。
[事実]
<\delta))
ここで
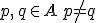に対して「事実」の
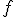を選択したものをそれぞれ
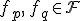とすると次の証明は容易です。
(i)
\ge{\epsilon-2\delta})
(ii)
<\epsilon-2\delta)
すなわち
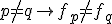が成立しこれは
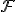の可算性に反します。
[(d) の証明]
まず first category set の定義を思い出します(こちらも完全に忘却のさな
たなのでありました。たしか「やせた集合(meager set)」という別名が。それ
では補集合は「ふとった集合」なのか！などと馬鹿なことを学生時代に言って
たような...)。
[Nowhere dense subset の定義]
位相空間の部分集合の閉包の内部が空集合のとき nowhere dense subset であ
ると言う
[First category set の定義]
位相空間において Nowhere dense subset の可算個の和集合を first
category set(第一類集合・やせた集合)と呼ぶ。位相空間の部分集合がが
first category であるためには、それが closed nowhere dense sets
の可算和の部分集合になれば良い
上の first category set の定義と注釈により
のもとで次の事実を証明すれば十分です。
)
を開稠密(open dense)集合の
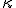列とするとき、やはり開稠密な
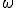列
)
が存在して
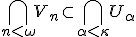
さて肝心の証明なのですが、全部書くと長くなるのと、細かい部分は詳細に
チェックすれば良いということで、結論のみを記述することとします。まず次
の集合(族)を準備します。
(i)
_{n<{\omega}})
. 有理数を両端とする開区間の数え上げ
(ii)
)
(iii)
)
すると
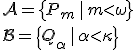
に対して前回の
Solovay の定理
を適用することが可能で、その結果得られる集合を
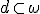として
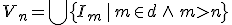
とするとこれが求めるものとなります。
{(e) の証明]
Suslin 直線と
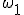-Suslin 木の関連を
記述した部分で
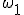-Suslin 木 は常に正規化可能であることを述べました。よって
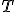を正規化した
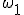-Suslin 木とします。
)
を仮定して、半順序集合
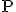として
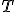自身をとります。ただし
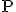の順序は
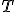の逆順序とします。言い替えると
~=~(T,{\ge}_T).)
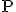が c.c.c を満たすのは
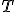が
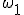-Suslin 木であることからの帰結です。さて次の集合列を考えます。
>\alpha\}\quad(\alpha<\omega_1))
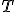が正規化されていることにより
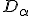は
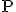で稠密です。ここで
)
なるフィルター
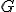を考えると、これは非可算な鎖(chain)となり矛盾です。
今回も主に Kenneth Kunen 著
Set Theory を参考にしました。
さてひとまず Martin の公理はおしまいにして(同値な言い替えとかまだまだ
やらなきゃいけないんですが)、次回からはしばらく、書こう書こうと思って
後回しになっていた「クラス」「正則性の公理」に関して記述して、さらに
Relativization や論理式の絶対性に関しての話題に切り替えて、ゲーデルの
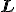に関する話題や forcing の準備としたいのです。
関連の話題に関しては
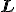と並行して扱う予定です。
