[集合論雑記目次]
実数直線
の通常の全順序構造が次の性質で一意に決定されることは良く知られています。
(a) 左右に非有界であるさてここで (c) の条件を次のように弱めることが可能かが大問題なのです。
(b) 完備である(任意の有界部分集合に対して上限と下限が存在する)
(c) 可算な稠密集合を含む(稠密とはなる
に対して
なる
が存在すること. この性質を separable と言う)
(c') 互いに素な開区間はすべて可算である一般の全順序集合で (c') の条件を満たすものを「countable chain condition を満たす」略して「c.c.c を満たす」言います。(c) が (c') を導 くのはほとんど明らかですが、この概念を一般化した Suslin 直線を定義します。
[Suslin 直線の定義]
次の条件を満たす全順序集合を Suslin 直線(Suslin line)と称する。
(a) 完備である
(b) c.c.c を満たす
(c) 可算な稠密部分集合は存在しない(separable でない)
[Suslin 仮説]
Suslin 直線は存在しないSuslin の仮説と、実数が実数の特徴付けの部分に記述した (a)(b)(c') の性 質で特徴づけられることは同等です。さらに Suslin 仮説は ZFC と独立であ ることが知られています。実際今後展開する
-Suslin 木と Suslin 直線には強い関連があります。
[定理]
まず Suslin 直線から-Suslin 木の存在と Suslin 直線の存在は同等である
[補題]
-Suslin 木
に対して次の性質をもつ
-Suslin 木
を構成可能である。
(a) 任意の補題の証明は省略しますがに対し
は可算無限。言い替えると x の「直接の後継(successor)」なる要素全体は可 算無限
(b)を極限数として
が
を満たすとき
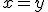
(c)<\alpha~\rightarrow~\exist{y\in{T^'_{\alpha}}(x<y)))
さてこの集合に適切な全順序構造を定義する必要があるのですがを
の枝(branch)全体からなる集合とする
さてここで構成したのとき
とし(
は枝
の要素を「下から」数え上げた
番目の要素。正則の条件の (b) によりこの順序数は極限数とはならない)。 このとき
はある
の要素の successor となるのでその順序を
で表すこととすると
のそれぞれの場合に対応して
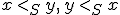
次にとすると
の順序の構成で使用した
は有理数の順序と同型に並べられているので
の同一の要素の successor となる
が存在し
を下方向には自明に延長した鎖を考え、それを含む枝の一つを考えれば証明完 了です。
さてまだ基本的な部分で書かなくてはならないこととして、
- 分割の性質.
- Almost disjoint family(「ほとんど素な集合族」とでも訳すのだろうか...)
- Lebesgue measure や Borel sets の基本的な性質
等があるのですが、このあたりは必要が生じたら言及ということで、そろそろ Martin の公理に入ろうと思いますが、今後話を進める場合、上に書いたよう な Combinatorial な部分の勉強不足がちょいとつらいところであります。余 談ですがうれしいことに、ここまでぼちぼち勉強すると、最初はちんぷんかん ぷんだったいくつかの巨大基数の定義(だけですが...)が理解可能となりまし て、列挙致しますと、
- 到達不可能基数(強極限な正則極限基数)
- 弱マーロ基数 κ(
が定常集合)
- 強マーロ基数 κ(
が定常集合)
- 可測基数 κ(κ上に κ-complete 超フィルターが存在する)
- 弱コンパクト基数 κ(
が成立する)
- 強コンパクト基数 κ (κ上の任意の κ-complete フィ ルターが κ-complete 超フィルターに拡張可能)
こうしてみるとデルタレンマの関連で、閉非有界集合を勉強したのはなかなか 良かったと再認識するのであります。
集合論雑記目次の参考文献に 「巨大基数の集合論・A.カナモリ著 渕野昌訳」 を追加しました。










