2005年6月

トップページに戻る谷山浩子さんのページ連絡先 kagami@evariste.que.ne.jp
2005年5月 2005年7月更新履歴と日記の先頭に戻る日記の目次集合論雑記目次
たかたにさん Y.Kumagaiさんはやしさん redcat_mathさん tri_iroさん
Stromdorfさんてなさくさん渕野さんの伯母野山日記
最近のコメント(50件) Twitter (@kagami_hr)

02/25 aiueo 01/01 かがみ 01/01 ゼルプスト殿下 01/01 かがみ 01/01 ゼルプスト殿下 05/10 かがみ

2005年6月29日(水)

健康診断本番
というわけで、本日健康診断だったのですが、もちろんもっていくべきものはおとといのうちに準備してあったのです。ただし二日に分けてとるのを、一回でごまかしてしまったのはないしょなのです。肝心の結果ですが、さすがにこの年になると色々壊れてくるらしく、どうも血糖量に問題があるようで、私は絶対に運動しない(育ちが良いので鉛筆より重いのを持ったことがない^^)人なので、これは食べる量を減らすしかありません。それはそうとおそらくこの 25年くらいで初の快挙が！
いままで「ちょいでぶ注意」だったのがついに「普通」になった(^^。
私の身長は大体 175cm なのですが、本日の体重は 76.2Kg。でもってこれ以上で「ちょいでぶ注意」の臨界値が 76.8Kg(^^。つまり 600g の差でセーフだったのです。まあこの身長での標準体重は 67Kg 程度ということで、まだ 10Kg も差があるのですが、無理にやせても意味ないので、再びぶたの道を歩まない様今後注意するということで満足しましょう。

2005年6月28日(火)

つくば出張
[10時30分とっても空いてる電車の中で]
今日は恒例となったつくばへの出張です。会議ではあんまり発言することもなさそうなので、開発の内職でもしてようかな(^^。
[19時45分とっても空いてる電車の中で]
とういわけで会議が終わったのが 19時過ぎ。いやはやおうちに着くのは 22時過ぎですなあ。ちなみに内職は結構はかどったのでした(^^。

2005年6月26日(日)

forcing について・Genericと名称(3回目)
[集合論雑記目次]

[2006年6月8日] 集合論雑記の強制法に関する部分はPDFファイルにまとめました。こちらの方が誤りが少なく、論理的にも整理されていると思います。詳しくは 2006年6月8日の記事を参照して下さい。
http://evariste.jp/kagami/diary/0000/forcing-1.0.pdf
http://evariste.jp/kagami/diary/0000/forcing-1.0.tex
[注意]下記証明では後で論ずる強制関係における等号の性質を暗黙に使用している部分があります。 　
昨日基本論理式以外に関する forcing の定義を行いましたが、本日は基本論理式に対する forcing の定義を記述します。尚、定義自体は、 Kenneth Kunen 著 Set Theory をそのまんま引用です。まず記述を簡単にするために $p\in\mathbb{P}~$ に対し $E\subset\mathbb{P}~$ が dense below $p~$ なる概念を定義します。
[Dense below $p~$ の定義]
$p\in{P}~$ とし $E\subset\mathbb{P}~$ が dense below $p~$ とは次の条件を満たすこと。
$\forall~q\le{p}~\exist~r\in{E}(r\le{q})~$
ここで未記述であったの定義を記述します。
[F1. $p||-\dot{X}=\dot{Y}~$ の定義]
$p||-\dot{X}=\dot{Y}~$ が成り立つとは次の F1-1, F1-2 の条件が成立すること。
F1-1. $\forall~(\dot{x},r)\in\dot{X}~(~~~~~\{q\in\mathbb{P}\,~|~\,~q\le{r}~\rightarrow~~~~\exist~(\dot{y},s)\in\dot{Y}~(q\le{s}~\wedge~q||-\dot{x}=\dot{y})\}~$

is dense below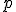 $p)~$
この条件を今後 $X\subset_{p}{Y}~$ と記述する.
F1-2. $\forall~(\dot{y},s)\in\dot{Y}~(~~~~~\{q\in\mathrm{P}\,~|~\,~q\le{s}~\rightarrow~~~~\exist~(\dot{x},r)\in\dot{X}~(q\le{r}~\wedge~q||-\dot{y}=\dot{x})\}~$
is dense below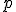 $p)~$
[F2. $p||-\dot{x}\in\dot{X}~$ の定義]
$p||-\dot{x}\in\dot{X}~$ が成り立つとは次の F2 が成立すること。
F2. $\{q\in\mathbb{P}\,|\,~~\exist~(\dot{z},r)\in\dot{X}~(q\le{r}~\wedge~q||-\dot{x}=\dot{z})\}~$ is dense below $p~$
これで昨日の P1〜P6 を証明する準備が整いました。まず P1 の証明です。

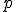
$p||-\varphi~\vee~\psi\cr~~\leftrightarrow~~p||-\neg(\neg~\varphi~\wedge~\neg\psi)\cr~~\leftrightarrow~~\forall~q\le{p}~(\mathrm{not}\,\,~q||-~\neg\varphi~\wedge~\neg\psi)\cr~~\leftrightarrow~~\forall~q\le{p}~(\mathrm{not}(q||-~\neg\varphi~\wedge~q||-\neg\psi)\cr~~\leftrightarrow~~\forall~q\le{p}~(\mathrm{not}(~~\forall~r\le{q}((\mathrm{not}\,\,r||-~\varphi)~\wedge~~~(\mathrm{not}\,\,r||-~\psi))))\cr~~\leftrightarrow~~\forall~q\le{p}~~~\exist~r\le{q}(r||-~\varphi~\vee~r||-~\psi)\cr~$
P2 の証明は P1 と同様な論理計算です。P3 はのとき dense below が dense below を導くことと F1, F2 の定義から得られます。P4 はの定義に従い論理式の数による帰納法によります。
1. まず $X=Y~$ を仮定すると $M^{\mathbb{P}}~$ の要素として $\check{X}=\check{Y}.~$ 従って強制法の等号の定義により $1\||-{\check{X}=\check{Y}}.~$ 逆方向は仮定を弱め $\exists{p\in\mathbb{P}}(p\||-{\check{X}=\check{Y}})~$ とし $x\in{X}~$ と仮定する. 存在記号の具体例を $p~$ とすると, $\check{X}\subset_{p}\check{Y}~$ が成立しているので, 任意の $q\in\mathbb{P}~$ に対して $r\le{q}~$ が存在し $\exists{\langle~\check{y},~1~~\rangle~\in~\check{Y}}(r\le{1}~\wedge~r\||-{\check{x}~=~~\check{y}}).~$ この $\langle~\check{y},1~\rangle\in\check{Y}~$ を一つ固定すると, $M^{\mathbb{P}}~$ のrankに関する帰納法の仮定により $r\||-{\check{x}=\check{y}}~$ から $x=y~$ が導かれる. 従って標準名称の定義により $x\in{Y}.~$
2. $x\in{X}~\,\Leftrightarrow~\,~\mathbb{1}||-\check{x}\in\check{X}~$ であることは forcing の $\in~$ に関する定義と 1 から簡単に得られます。
3. 論理積と否定に関する帰納法のステップも容易です。
4. 最後に $\varphi(x)~$ を $\Delta_0~$ 論理式とするとき $\forall~x\in{y}\varphi(x)~\,\Leftrightarrow~\,~~~1|=\forall\dot{x}\in\check{y}\varphi(\dot{x})~$ を証明します。まず定義により
  $1|=\forall~\dot{x}\in{\check{y}}(\varphi(\dot{x}))~~\,\Leftrightarrow~\,~~~\forall~\dot{x}\in{\check{y}}(1|=\varphi(\dot{x}))~$
  ところが上式の右側の全称記号は $M^{\mathbb{P}}~$ 上の(forcing とは関係がない)通常の解釈なので
  $\forall~\check{x}\in{\check{y}}(1|=\varphi(\check{x}))~~\,\Leftrightarrow~\,~~~\forall~x\in{{y}}(1|=\varphi(\check{x}))~$
  と書き直すことが可能です。 $\varphi(x)~$ は $\Delta_0~$ 論理式だったので、帰納法の仮定により
  $\forall~x\in{{y}}\varphi(x)~$
これで前日の P4 の証明が完了しました。P5 は長くなりそう！書くのはいつになるのだろう。でも一番肝心なことなので証明しないと議論が進まないし...。いやはや面倒ですなあ(笑)。

2005年6月25日(土)

forcing について・Genericと名称(2回目)
[集合論雑記目次]

[2006年6月8日] 集合論雑記の強制法に関する部分はPDFファイルにまとめました。こちらの方が誤りが少なく、論理的にも整理されていると思います。詳しくは 2006年6月8日の記事を参照して下さい。
http://evariste.jp/kagami/diary/0000/forcing-1.0.pdf
http://evariste.jp/kagami/diary/0000/forcing-1.0.tex
前回集合論(ZFC)の推移的モデル $M~$ とそれに属する半順序集合 $\mathbb{P}~$ に対して、P-名称からかるクラス $M^{\mathbb{P}}~$ と $M~$ の要素の標準名称を定義しましが、ここで P-Generic $G~$ の標準名称 $\dot{G}~$ を定義します。
$\dot{G}~=~\{(\check{p},p)~|~p\in\mathbb{P}\}~$ を $\mathbb{P}~$ -Generic の標準名称と呼ぶ
$\dot{G}~$ は特定の P-Generic(存在してもしなくても)とは無関係に $M~$ 上定義可能であることが重要です。
さて、これから forcing の定義を行いその基本性質を記述したいわけですが、完全な定義する前に forcing が満たすべき性質を列挙したいと思います。
まず、集合論の言語に P-名称、すなわち $M^{\mathbb{P}}~$ の要素をすべて定数として追加した言語を考え、この言語を forcing language と呼ぶこととします。さて $\varphi(x_1,~x_2,~\cdots~,~x_n)~$ を論理式とし、自由変数はすべて $x_1,~x_2,~\cdots~,~x_n~$ に現れるものとします。このとき $p\in\mathbb{P},~\dot{x_1},~\dot{x_2},~\cdots,~\dot{x_n}\in{M^{\mathbb{P}}}~$ (名称を表す対象式には \dot を付加する場合が多い)に対し強制関係
$p||-\varphi(\dot{x_1},~\dot{x_2},~\cdots,~\dot{x_n})~$ ( $p~$ は $\varphi(\dot{x_1},~\dot{x_2},~\cdots,~\dot{x_n})~$ を強制する)
を今日は一部分定義して、証明抜きで基本的な性質を列挙します。
[forcing の定義]
F1. $p||-\dot{X}=\dot{Y}~$ の定義は次回以降
F2. $p||-\dot{x}\in\dot{X}~$ の定義は次回以降
F3. $p||-\varphi\wedge\psi~\,\Leftrightarrow~\,(p||-\varphi\,\,\mathrm{and}\,\,p||-\psi)~$
F4. $p||-\neg\varphi~\,~\Leftrightarrow\,~(\mathrm{not}\,~q||-\varphi\,\,~~\mathrm{for~all}\,\,q\le{p})~$
F5. $p||-\forall{\dot{x}}\varphi(\dot{x})\,\Leftrightarrow\,~~(p||-\varphi(\dot{x})\,\,\mathrm{for~all}\,~\dot{x}\in{M^{\mathbb{P}}})~$
肝心の F1, F2の定義は案外難しいです(少なくとも私にとっては...)。ここで F1,F2 の性質に依存するので、もちろん今証明を記述出来ないのですが、 forcing の重要な性質をいくつか列挙します。
P1. $p||-\varphi\vee\psi\,\Leftrightarrow\,~~\forall{q\le{p}}\exist{r\le{q}}(r||-\varphi~\vee~r||-\psi)~$
P2. $p||-\exist{\dot{x}}\varphi(\dot{x})\,\Leftrightarrow\,~~\forall{q\le{p}}\exist{r\le{q}}~~(\exist\dot{x}\in{M^{\mathbb{P}}}(r||-\varphi(\dot{x})))~$
P3. $p||-\varphi~\wedge~~(q\le{p})~\,\Rightarrow~\,q||-\varphi~$
P4. $\varphi~$ を $\Delta_{0}~$ 論理式とするとき $\,\,\,\,\,\,\,\,M|=\varphi(x_1,~x_2,~...,~x_n)\,\Leftrightarrow\,~~~\mathbb{1}||-\varphi(\check{x_1},~\check{x_2},~\cdots,~\check{x_n})~$
P5. $\varphi~$ を ZFC の公理とするとき $\mathbb{1}||-\varphi~$
P6. $\mathrm{ZFC}|-\varphi\,\Rightarrow\,\mathbb{1}||-\varphi~$
ここで $\Delta_0~$ 論理式は次の様に定義されます。

D1. $x=y,~x\in{y}~$ は $\Delta_0~$ 論理式
D2. $\varphi,~\psi~$ を $\Delta_0~$ 論理式とするとき $\varphi\wedge\phi~$ も $\Delta_0~$ 論理式
D3. $\varphi~$ を $\Delta_0~$ 論理式とするとき $\neg\varphi~$ も $\Delta_0~$ 論理式
D4. $\varphi~$ を $\Delta_0~$ 論理式とするとき $\forall{x}\in{y}\varphi(x)~$ も $\Delta_0~$ 論理式

さらにそんなに難しくはないのですが、個人的にか結構気になっていた基本的な事項、即ちP-Generic の標準名称 $\dot{G}~$ が強制関係において、確かにGenericの性質を満たすことも示したいと考えています。即ち下記の証明を記述します(最初なのでかなりくどい記法になっています)。
$\mathrm{G1.}\,\mathbb{1}||-\dot{G}\subset\mathbb{\check{\mathbb{P}}}\cr~~\mathrm{G2.}\,\mathbb{1}||-\dot{G}\,\,\text{is~a~filter~on}\,\,~~\mathbb{\check{\mathbb{P}}}\cr~~\mathrm{G3.}\,\mathbb{1}||-[(\dot{D}\subset\check{\mathbb{P}}~\,\,~~\text{is~dense~in}\,\,~~\check{\mathbb{P}})~\wedge~\dot{D}\in\check{M}~~\,\rightarrow\,~\dot{G}\cap\dot{D}\neq{\emptyset}]~$
うるさいこと言うと $\mathbb{P}~$ の順序関係を $R~$ とした場合 $\check{R}~$ が $\check{\mathbb{P}}~$ の順序関係であることが強制される事実も示す必要もあります。
次回は F1, F2 の定義をきちんと行い、比較的簡単な P1, P2, P3, P4 を証明する予定です。ちなみに P5 の証明はそれ以前のものに比べてはるかに難しいです。

2005年6月23日(木)

Tigerおまけ電卓
OSのおまけに電卓が付いてくることは結構多いのですが、実用的に使用出来るものは案外少ないと思います。そもそも私は電卓に関して案外わがままなところがありまして、次の条件が満たされないといまいち(絶対に？)使用する気分にならないのです。
逆ポーランドでないと絶対にだめ。
プログラマー向け 16, 10, 8, 2進数が使用出来ないとだめ。
cos, sin, exp 等の初等超越関数近似機能も欲しい。
ところが本日偶然、どうせTigerのおまけ電卓もたいしたことないんだろうな〜、と思って電卓を起動してみたのですが、これがホントに素晴らしいのですよ(^^。まず RPN (逆ポーランド入力)を使用出来るモードがちゃんとありまして、さらにいわゆる科学技術計算モード、プログラマーモードもありまして、今まで RPN のフリーソフトを色々と集めて用途により使い分けていたのですが、今後はこれ一つですべての用途に使えそうなのです。うーん素晴らしい(^^。

2005年6月22日(水)

HPと間違われる
お昼休みにうだうだしてたら、会社の取締役の T さんが私のところに来まして、「あれっ、かがみさん HP のノート使ってるんですか」と言うのです。

なに〜、えっちぴーだと〜！！なんと失礼な(=_=)
どうも遠くから見るとこれに似てるということなのです。でも似てるっていったって、単に銀色っぽいだけじゃん(^^。格調高い PowerBook と間違えないでちょうだいよ！。
ところで Tさんによりますと、こんど上のリンクの HP 4800/CT シリーズを買おうかな〜、という話なのですが、いつの間にか机の上の PowerBook が HP と入れ替わっていたらどうしよう(^^。

2005年6月21日(火)

多項式補完の謎
私が勤めている会社ではいろいろなデーターを収集する機材を開発しているのですが、実際の現場では種々の原因により、まれにデーターを収集しそこなう場合もあるのです。その場合データーを補完する必要が発生する場合もあるのですが、詳しい人の話によりますと、
データーの補完は、通常 1次から 5次までの多項式を使用して行う場合が多い
そうなのです。うーむどうして最大 5次なのだろう...。ここで普通(普通じゃないか^^)思いつくのは、「5次以上の方程式は一般に四則演算と冪根では解けない」ということで、もしかして実測データーというのは例えば楕円関数(5 次方程式は楕円関数を使えば解ける)を使用すると良い近似が出来るのかな？
いやいやもちろんそんなことがあるはずがなく、経験的に 5次位で十分というのがほんとの理由なのですが、「5次方程式」というとすぐに「代数的な観点から反応してしまう」というのも、長い間の習性とはいえ、実生活では役に立たないことおびだたしいですな(^^。

2005年6月18日(土)

人様緊急データー復旧作業
本日の 21時頃食事も終ってうだうだしていたら、突然家族全員知り合いの人 (Aさんとします)から電話が。話を聞くと、彼が使っているシャープのノート PC が突然ブートしなくなり、Windows XP を再インストールしたけどうまくゆかず、明日どうしても使用したいのと、中に入っているデーターがなくなってしまうと大変面倒なことになる、ということなのです。
「えーっと、領域は C, D に分割してあるのですか」と聞いたところ、そうなっているそうで、再インストール時にデーターが置いてある D は壊していないはずであるということなのです。いずれにしても話を聞いただけではらちがあかないので、奥様に運転お願いして車で 30分位の A さんのお宅に出陣しまして、到着が 22時。もってったものは、
1. PowerBook --- これは調べものが必要な時 AH-K3001を使ってネットに接続するため。
2. FreeBSD/X24 --- これは A さんのノート PC のハードディスクをマウントして調べるため。
3. 2.5inch HDD/USB 変換箱 --- 2 で使うため。
4. USB たこ --- 2 で使う場合ノートでは電源が不足する可能性があるため。
5. 余っている 2.5inch 30Gハードディスク --- 何かのときに役立ちそう。
6. ドライバーセット --- HDD を外したりする場合必要かも。
でして、鞄二つにつめこんでなんか大変な騒ぎになってきました(^^。
一番気になったのは、ハードディスクが簡単に外れるかということだったのですが、幸いねじ二つだけで取れる様な機構になっていまして、その点はほっとしたのです。さっそく取り外して IDE/USB 変換箱経由で X24に接続したところうまいこと認識されまして、デバイス名が /dev/da0。Fdisk で調べたところ、確かに二つパーティションが切ってあります。でも XP なのに FAT32形式だったのにはちょっとびっくり。な〜んだ、それなら PowerBook だけ持ってけば良かったかな。それはともかく、まずは C ドライブをマウントしてみようということで、次のコマンドを実行です。
```
# mount -t msdos -oro /dev/da0s1 /mnt
```
これはうまいことマウント出来まして、確かに C ドライブっぽい内容です。よしよしこれならば D ドライブも簡単にマウント出来て、とりあえずデーターの退避は簡単に出来るであろうと思ったのです。ところが /dev/da0* のどれを使っても、D ドライブをマウント出来ないのですよ！。
うーむ、もしかして D ドライブの先頭のメタ情報が壊れているとするととっても面倒、といいますか、修復不可能だろうな。困ったな〜、と思いつつ次なる作戦は、持って行ったハードディスクを A さんのノート PC に入れ、それに Windows XP をインストールして、A さん所有の調子が悪いディスクを USB 経由で刺してみようかということです。インストールするのに一時間近くかかりそうで、すでに時間は午前零時を回ったのですが、乗りかかった船！ここでやめる訳にはいきません。世間話をしているうちにインストールも終了しまして、さっそく A さんのディスクを USB 経由で刺したところ、おお！
E ドライブと F ドライブが見えるではないか(^^。
さらに間違いなく F ドライブの内容は、もともとの D ドライブの内容であるとのこと。これでやっとこデーターを救うことが出来そうです。ということで、 F(A さんの調子が悪いディスク)から C(私のハードディスク)に重要そうなフォルダー全部まとめてコピーしようとしたのですが、半分予想していた通り途中でエラーが発生します。特定のファイルが読めないようです。そこでちと面倒だったのですが、コピー不能なフィアルはあきらめてもらうということで、一つ一つ確認しながらファイルをコピーを行ったのですが、幸いにして、コピー出来なかったファイルは大して重要でないものばかりだったのです。でも、なかなかスリルのあるコピー作業でした(^^。
これですべてがうまく行った様ですが、問題は今 A さんのノート PC に入っていて、非常に調子よく動作しているディスクは私のものだということで(笑)、まあ私にとっては緊急に必要があるものでもなく、A さんにとっては「明日どうしても必要」なものだそうなので、落ち着くまで一月間程度、そのままの状態でお貸しすることにしました。
ちなみに Aさんはちともったいなさそうにしていたのですが、「今まで使っていたハードディスクは破棄して新品を購入しないと、また同じことになりますよ！それからバックアップはまめにとること！！」と念を押したことはもちろんです(^^。作業終了が早朝 2時で帰宅が 2時30分。980円の IDE/USB 変換機君、大活躍でした。

2005年6月17日(金)

iPod shuffle

巨大ヘッドフォンを繋いでみた

今日の朝になって突然モカちゃんいわく。「本当は iPod mini が欲しかった！」。
うーん、そういうことは早めに言わないと〜(^^。ところで iPod mini は一番安いのでも二万円以上しまして、小学生への誕生日プレゼントとしては高すぎますし、そもそもそんなにお金がありません。でも考えてみると、そんなにたくさん CD とか持っている訳でもないのに、4G もの容量が必要とは思えません。まあそういうのが欲しくなる年頃であることは分かるので、これも小学生にはちと高いとは思ったのですが、お昼休みに 512M の iPod shuffle を一万円ちょっとで購入です。
おうちに帰ってさっそく、「一日遅れのプレゼントで、しかも iPod mini じゃないんだけど〜」と見せたところ、モカちゃん大喜びで言うには、
あれれれっ、それ iPod mini じゃないの？
あはは！やっぱり違いが分かってなかったのね(^^。というわけでご家族様 PC にiTunes をダウンロードして、さらにモカちゃん所有の CD を AAC(192Kbit だよ！！) に変換して iPod mini にダウンロードして聴いてみたのですが、それなりの音は出るようで、なんか私も欲しくなって来たのですが、いやいやこれ以上散財するのはぜったいぜったいに避けなければいけません(^^。

2005年6月16日(木)

モカちゃん誕生日
今日はモカちゃん 12才の誕生日。みんなでお祝いのケーキを食べたのですが、肝心のプレゼントは、「特に欲しいものないな〜」というので今年は特に上げないつもりだったのですが...。

2005年6月15日(水)

健康診断
今年も健康診断の日がが近づいてきました。いやいや前みたいなねたにするつもりはないのですが、一つだけ大きな謎があるのです。つまりですな！洋式のトイレで検便のねたを採取するのは非常に難しい、ということに関して前回非常に論理的かつ精緻なる考察を行いましたが、要するに沈んでしまうと後が非常に面倒になるということなのです。そこでなんとか沈まない算段を行う必要が生じるのですが、「大きいのは沈みやすい」ということは経験的に良く知られている事実であると思います。というわけで、最初の部分を「切って」小さい状態のを浮かせて採取する手法が一般的な訳ですが、ここで大いなる謎が...。
おっきくてもちっちゃくても比重は同じはずなのに、どうして浮いたり沈んだりするのか(^^。
むむむむむっ、これは科学史上最大の謎なのでは！！。リーマン予想より難しいかもしれない。もしこの大問題に対する納得のゆく理論が構築出来れば、人類最大の知的偉業が達成されるとともに、健康にもとっても役立つということで、ノーベル医学賞生理学賞の受賞は間違いありません。それにしても難解な(笑)。どこから手をつければ良いのだろう(^^。

2005年6月13日(月)

お休み
今日はとっても体調が悪くて、会社休んで一日寝てました。休日中数学で無理しすぎてるのか？

2005年6月12日(日)

forcing について・Genericと名称(1回目)
[集合論雑記目次]

[2006年6月8日] 集合論雑記の強制法に関する部分はPDFファイルにまとめました。こちらの方が誤りが少なく、論理的にも整理されていると思います。詳しくは 2006年6月8日の記事を参照して下さい。
http://evariste.jp/kagami/diary/0000/forcing-1.0.pdf
http://evariste.jp/kagami/diary/0000/forcing-1.0.tex

Forcing(強制法)という概念は、連続体仮説の ZFC からの独立性と選択公理の ZF からの独立の証明において、1963年に Paul Cohen により提唱された、極めて斬新的な手法です。ここでは歴史的な順序は追わず、最初に Generic なる概念を定義します。まず半順序集合の稠密部分集合(dense subset)の定義から。
[稠密部分集合の定義]
半順序集合 $\mathbb{P}~$ の部分集合 $D~$ が $\mathbb{P}~$ で稠密とは次の条件が成立すること。
$\forall~p\in\mathbb{P}~\exists~d\in{D}~(~d~\leq~p)~$
そして Generic の定義。
[Generic の定義]
$\mathbb{P}\in{M}~$ を半順序集合とし最大元 $\mathbb{1}~$ を持つとする(半順序構造は明記しないが、これも $M~$ の要素とする)。 $\mathbb{P}~$ 上のフィルター $G~$ が $M~$ 上 $\mathbb{P}~$ -generic とは次の条件を満たすこと。
$D\subset\mathbb{P}~$ が $D\in{M}~\wedge~(D\,\,~\text{is~dense~in}\,\,\mathbb{P})~$ を満たすとき $G\cap{D}\neq{\emptyset}~$
興味ある Generic $G~$ は $M~$ の要素にはなりません ( Martin の公理参照 ) 。それではどこの要素となるのかと言いますと、 $M\in{V}~$ が ZFC の可算モデルの場合は $V~$ の要素となることが分かるのですが、ZFC の可算モデルの存在はゲーデルの不完全定理により ZFC からは証明出来ません。しかしながら証明しようとしている文脈で必要とする「有限な」公理系に対するモデルの存在は証明出来るので、それを考えるというアプローチが考えられます。それにもかかわらず、可算モデルのみを考えるのは色々不便な面があるのと、実際には $V~$ の要素である半順序集合に対する仮想的な Generic $G~$ を考え、それにを $V~$ に付け加えた「仮想的な拡大」 $V[G]~$ を考えて推論を行うことは超数学的に正当な推論のちょっと省略した記述である、ということが(おそらく Boolean-valued model による手法により)知られています。そこで当面「generic が存在しない」という点に関しては気にしないで推論を進めることとします。
さて Generic G はフィルター(特に超フィルターともなると)というだけで仮想的な感じが強いのですが、Generic なる条件を考えることにより、さらに仮想的な雰囲気が強まり(竹内外史先生の言葉によると「夢の世界」)、その性質を具体的に記述するのは難しい感じがしますし、事実そうなのです。
ただし、具体的な性質は(少なくとも $M~$ からは)定まらなくとも、forcing language という $M[G]~~$ の要素の「名称」(これは $M~$ で定義可能)の集合(クラス)なるもの $M^{\mathbb{P}}~$ を考え、個別の $p\in\mathbb{P}~$ に対して、その名称間の論理式に対する強制関係(forcing relation)を考えることにより、 $M[G]~$ の要素間の「性質」に関して調べることが可能である、というのが今後何回かに分けて記述する予定である forcing の主眼なのです。正確な定義を一つもしないのもなんなので、まずは $\mathbb{P}~$ -名称(P-name)の定義を。
[P-名称(P-name)の定義]
$M~$ を ZFC の推移的な(集合またはクラス)モデルとして $\mathbb{P}\in{M}~$ を最大元をもつ半順序集合(順序構造も $M~$ の要素)とする。このとき次の定義を行う。
(1) $\emptyset~$ は $P~$ -名称である。
(2) $\beta<\alpha~$ に対する $\mathrm{rank}(\beta)~$ までの $P~$ -名称が定義されていたとする。このとき $u~$ が $\mathrm{rank}(\alpha)~$ の $P~$ -名称であるとは
$\forall~v\in{u}~\exists{x\in{M}}\exists{p\in\mathbb{P}}((x~$ is a P-name of $\mathrm{rank}(x)<\alpha)~$ $\wedge~v=(x,p))~$

(2)をもう少し分かりやすく記述すると
(2') $u~$ is a relation and $\forall~(x,p)\in{u}((x~$ is a P-name) $\wedge~p\in\mathbb{P})~$
名称 $u~$ に対しその domain は通常の定義です。
$\mathrm{dom}(u)=\{x\in{M}~|~\exists~p\in\mathbb{P}((x,p)\in{u})\}~$
P-名称全体の集合(クラス)を $M^{\mathbb{P}}~$ と記述します。 $M^{\mathbb{P}}~$ は Generic と無関係に定義可能であることが重要です。気分的には $(x,p)\in{u}~$ というのは $x~$ が $p~$ 「程度」 $u~$ の要素であるという感じです。特に、上の定義に現れる $p\in\mathbb{P}~$ を全部 1 として domain をもともとの集合の要素に限定することにより、 $M~$ の要素 $x~$ の「標準名称」 $\check{x}~$ を定義することが出来ます。通常は $\check{x}~$ は \check{x} なる記法を使うのですが mimeTeX で \check が使えないので、この日記では \tilde で代用します。
[標準名称の定義]
(1) $\check{\emptyset}~=~\emptyset~$
(2) $\check{x}~=~\{(\check{y},1)~|~y\in{x}\}~$
$M~$ の要素をその標準名称に対応させることにより、 $M~$ を $M^{\mathbb{P}}~$ に埋め込んで考えることが出来ます。

2005年6月10日(金)

OmniGraffle 4 Beta
OmniGroup から将来の Intel Mac のサポートに関して何らかの声明が出てるかな〜、とアクセスしたところ、それに関しては特に記述がなく、 OmniGraffle Version 4 ベーター版がリリースされていました。さっそくダウンロードして使ってみたのですが、かなりユーザーインターフェースが変化していた驚きました。慣れるまで少々時間がかかりそうです。ベジェ曲線(Bezier curves)のサポートが一番の売りかな。今までの版では、見栄えの良い曲線を書くのにちと苦労が多かったので、これは助かります。
夏頃に正式版がリリースされ、OmniGraffle 3 Professional からのアップグレードは49.95ドル。きっと払っちゃうんだろうな(^^。

2005年6月8日(水)

Re:宇宙の絶対静止系
最近読んだ雑誌「日経サイエンス2005年6月号・ビッグバンをめぐる6つの誤解」の記述によりますと、背景輻射との関係において宇宙の絶対静止座標は定義可能であると書いてあります。トップ記事でわざわざ書いてあるのでうそではないと思いますし、直感的にもなんとなくそうかな〜とは思うのですが、まあこちらの方は全くうといので、書いてあることを信じているだけというのが本当のところだったりします(汗)。分かりやすくなくってごめんなさい(^^。
つまんない知識を書きますと、アインシュタインの一般相対論の一つの解として「ゲーデルの回転宇宙」というものがあり、これは明確にマッハの原理を否定しています。つまり「回転している」という概念は「外から眺めなくとも」宇宙それ自身で定義可能で、おそらく現実の観測された宇宙とは矛盾すると思われるのですが、その解釈を採用すれば、回転にそった「移動」として絶対静止は定義可能なように思われます。ちなみに回転に逆らって逆方向に移動すると、過去への時間旅行ができるそうな。←理論的な根拠が全然分かっていないのでうそだったらさらにごめんなさい(^^。
＃ゲーデルはもちろん「ゲーデルの不完全性定理」のクルト・ゲーデルです。
＃さすが20世紀を代表する天才数学者！！手広いです。

2005年6月7日(火)

集合論古書
「かがみさん集合論が好きだし、ねたにもなりそうなので」と会社の同僚の N さんがくれた本の題名は「能代清著・極限論と集合論」。1944年に第1刷が発行されたもので、N さんが購入されたのは第11刷で 1960年発行のものなのです。ちなみにお値段は 180円(^^。さすがに戦争中の本ということで、平仮名とカタカナの使い方が今とは逆になっています。

右の写真をおっきくして見ると、左上に「実数の濃度は可算ではない」証明らしきものが書いてあることが分かりますが、それより面白いのは、やっぱり「べるんしゅたいんノ定理(*)」ですね(^^。全部カタカナで書いてあるとそんなに違和感はないと思うのですが、外国の人の名前が平仮名というのはなかなか面白いです。実数の色々な部分集合の性質をモチーフに、一般集合論の概念を丁重に記述して内容のようです。そういえばこの時代にはまだ「連続体仮説」のZFCからの独立性は未解決であったわけで、実際に「未解決である」との記述があります(1963年に独立性が証明された)。
とても貴重な本を頂き、ほんとにありがとうございます(^^。
(*)[ベルンシュタインの定理]
集合 X から Y への一対一の写像と Y から X への一対一の写像が存在するとき、X から Y への一対一かつ上への写像が存在する。

2005年6月6日(月)

Quarts 2D Extreme を有効にしてみる
とある情報によりますと、Tiger の隠し機能で Quarts 2D Extreme を有効にする手段があるそうです。この機能を有効にすると、GPU の Direct X9 サポートによっては 2D 画像の書き込みの一部をグラフィックチップに依頼することが可能になり、体感速度が向上する場合があるそうな。ただしおうちの一世代古い PowerBook の GPU がサポートしているかはよく分かりません。
というわけで調べてみたのですが、
りんご→このMacについて→詳しい情報
なるパスで調査可能(システムプロファイルと言うそうな)だそうで、実際にやってみると、使っている GPU はGeForce FX Go5200 なるもので、うまいこと対応可能なようです。隠し機能の使い方は、
# defaults write /Library/Preferences/com.apple.windowserver \
Quartz2DExtremeEnabled -boolean YES
なるコマンドを実行してリブートすれば良いそうで、実際に行ったところ、スナップショットのごとくちゃんと機能が有効になったようです。
ただし肝心の速度はと言いますと、まだいまいち実感がないというのが本音だったりします。
＃もし速くなっててもあっという間に慣れてしまうしね(^^。

2005年6月5日(日)

謎の名前解決不調
二三日前からとある日記系サーバーがおうちからアクセス不能になっていたのです。まあこういうサーバーは予告無くアクセス不能になる場合が良くあるので、今回もそうかな〜、と思っていたのですが、それにしてはだめな期間が長過ぎます。
うーむ、昨日からアンテナもどきを作ろうとして、変なユーザーエージェントで何回もアクセスしたから出入り禁止になったか、と思って色々調べてみたのですが、どうも名前解決の段階で失敗していると思われるのです。ということは出入り禁止ではなさそうなのですが、不思議なことには、レンタルサーバーの方で名前解決を行うとうまくゆくのです(^^。
そういえば最近他のページを見に行く場合も、なんか一回目がやけに遅くなった様な気がします。そこで、試しにおうちのサーバー(FreeBSD/R30)の named を再起動したら、すべてがうまくゆく様になりました。うーん、良く分からないのですが、named ってあんまり長時間起動し続けると不調になる場合があるのかな。今後は一週間に一度くらい再起動した方が良いのかも知れません。

2005年6月4日(土)

うたたさんのアンテナ
5月いっぱいでうたたさんのアンテナの公開が中止されるというアナウンスがされていましたが、本日本当に公開中止されたようです。色々とご苦労が多かったと推測されるのですが、とても便利に使わせて頂いていましたので、ちょっと残念なことは事実です。先月中に良く遊びに行くところに関しては全部ブックマークに保存しましたので、当面こちらで運用することになりそうです。
ただし存外数が多くなってしまったので、全部手作業で更新チェックを行うのは難しいかも知れません。もしかすると自前のアンテナを作成する必要があるかな。個人的には無料のサービスのアンテナを自分で管理するのは余り好まないので(今まで便利に使わせてもらったのに失礼)、自作ということになりますが、定期的に w3m で取ってきて、上や下の方の広告等を head やtail コマンドで削除し、diff に渡せばなんとかなるかな。でも、最近とみにずぼら化しているので、作る気力が湧くかどうか微妙なところですが...。
どうも長年お世話になりました(^^。

2005年6月2日(木)

趣味の集合論のススメ
おすすめしても誰ものってこないとは思うのですが(^^。でもホントに集合論って、いろんな数学の中で「楽しむ」という観点からは、一番適した分野かな〜と思うのです。実際、近代以降の代数学や幾何学・解析学等の分野は必要な予備知識が多すぎて、いい年した素人が空いた時間に趣味で勉強して、表面的にでも20 世紀以降の偉大な成果を理解することはとても難しいと思うのです。
もちろん私がこの一年半くらいで勉強した集合論の内容などは初歩の初歩、そのまた初歩ですし、さらに今のところ、肝心な実数の細かい性質(解析学もっとまじめに勉強しとけば良かった...)とか、分割の性質等、面倒そうな部分をすっとばしているのも事実なのですが、それでも少しは集合論という学問の方向性というものが見えてきた様な気がするし、色々な定理の証明というか意味を理解した瞬間がなんともうれいしいのですよ！！。理論の性質上「逆理的」な結果に驚くことも多いしね。
集合論におけるゲーデルの業績とか Cohen の forcing というのは、確かに天才的な発想と、言語や論理それから計算に対する卓越した洞察力がなければ絶対に達成不可能な偉業なのですが、個人的な感想としては、他の数学の分野の偉大な業績に比べれば「理解して楽しむための技術的な困難さ」は少なくてすむ様な気がします。要するに予備知識が余りいらない場合もあるのです。実際には書きなぐったノートの山が出来ている(しかも他人が見たら意味不明な図がたくさん書いてあったりする)のですが、感覚的にはアイディアや証明を読み物として楽しめるというイメージです。誤解が無いように書いておきますが、集合論が簡単であるとか、技術的な難しさが他の分野ほどではないなどということではありません。ただ楽しめる(しかもとんでもなく楽しい！！)分野まで到達するのに、他の分野に比してやや困難が少ないと思われるということです。
建前としては集合論の勉強を始めるには、高校程度の数学の知識があれば十分なのですが、一応知っていると楽出来る概念としては、　
- 初歩的な代数の知識。線形代数とか群や可換環の定義くらいは。
- 初歩的なトポロジーの知識。位相構造とフィルターとか。特にフィルターは集合論においてびっくりするほど活躍するので、トポロジーとの関連の直感があったほうが後が楽。
- 実数の基本的な性質。特に積分論。これは私全然だめなのですが、ルベーグ測度やボレル集合等の研究は、現代的な集合論のトピックとして一番面白いものの一つらしいです。
- 後大切なのは、論理や証明がどのような方法で形式化されているかの認識でしょうか。このあたりをはずすと「とんでも」方面に向かってしまう恐れがあるかも知れません。まあ数学のとんでも系の人って、大体形式と解釈を混同してますから。形式的な記述とその解釈に関するある種の感性は必須だと思います。
あたりでしょうか。やっぱり大学一二年程度の数学の基本的な知識は必要かな。というわけで、素人が好き勝手なことを書きましたが、ホントに面白いんですよ！！集合論って。お薦めです(^^。
＃大学一二年なんて書いたくせに、最近モカちゃん(小学校6年生)に
＃数の計算の速度や正確さでで負けてるのは絶対に内緒なのでした(^^。

2005年6月1日(水)

番外編・やっぱforcingではまる
[集合論雑記目次]
案の定forcingの意味が全然分かってなかったようで、連続体仮説の独立性の証明を読んでて、元の半順序集合のc.c.c条件が基数の絶対性を導く部分における次の証明が直感的に分かんなくって半日くらいはまりました。
$M~$ を集合論の推移的なモデルとして、 $\mathbb{P}\in{M}~$ を最大元 $1~$ を持ち c.c.c(countable chain condition)を満たす半順序集合、 $G~$ を $M~$ 上 $\mathbb{P}~$ -generic とする。ここで $X,~Y\in{}M,~f\in{M[G]}~$ で
$M[G]~$ で $'{f}~$ is a function from $X~$ to $Y'~$ が成立していることとする。
このとき
$\varph\in{M},~\varphi:~X~\rightarrow~\cal{\mathbb{P}}(Y)~$ が存在して $\forall~x\in{X}(f(x)\in{\varphi(x)})~$ が成立し、さらに $\forall~x\in{X}(|\varphi(x)|\le\aleph_0)~$ が成立する。
証明は「理解してしまえば」簡単で、 $f~$ の名称を $\dot{f}\in{M^{\mathbb{P}}}~$ として $p\in{G}~$ を
$p||-'\dot{f}~$ is a function from $\check{X}~$ to $\check{Y}'~$
が成立するようにとり
$\varphi(x)~=~\{y\in{Y}\,|\,\exist{q\le{p}}(q~\rm{||-}~\dot{f}(\check{x})=\check{y})\}~$
(*) \check が mimeTeX で使えない様なので \tilde で代用
とすれば良いのですが、どうしてこんなことしなけりゃいけないのか全然分からなかったのですよ(汗)。つまり $f(x)\in{Y}~$ が成立するので $\varphi(x)=\{f(x)\}~$ として何が悪いのか悩みに悩んだのです(恥)。ということは、なんとか分かってから ( $f(x)~$ の値は $M~$ では確定しない。というより $f~$ に関連することを名称経由でなく $M~$ で言及してはいけない)考えると、やっぱりforcingについて全然理解してないことが明白になったわけで、「大体分かった」というのは全然分かっていないという「理論」を自ら実証したのでした。いずれにしても、まだ色々手抜きや勘違いしてる可能性もあるのですが、今は「連続体仮説のZFからの独立性」を理解した気分になっていまして、集合論の勉強を始めた一つの目標を達成した訳で、個人的にはとってもうれしかったりします(^^。